【凸分析】
<aside> 🏛️
凸的定义：函数中，空间中，集合中
</aside>
-
【graph图】：函数图像，曲线，曲面可以看成空间点集合。
$$ gph (f)=\left\{\begin{pmatrix}\bm x\\\beta\end{pmatrix}\subset\mathbb R^{n+1}\mid \beta= f(\bm x),\bm x\in \Omega\right\}. $$
-
【epigraph上图】：函数的上方的点的集合
$$ epi(f)=\left\{\begin{pmatrix}\bm x\\\beta\end{pmatrix}\subset\mathbb R^{n+1}\mid \beta\ge f(\bm x),\bm x\in \Omega\right\}. $$
-
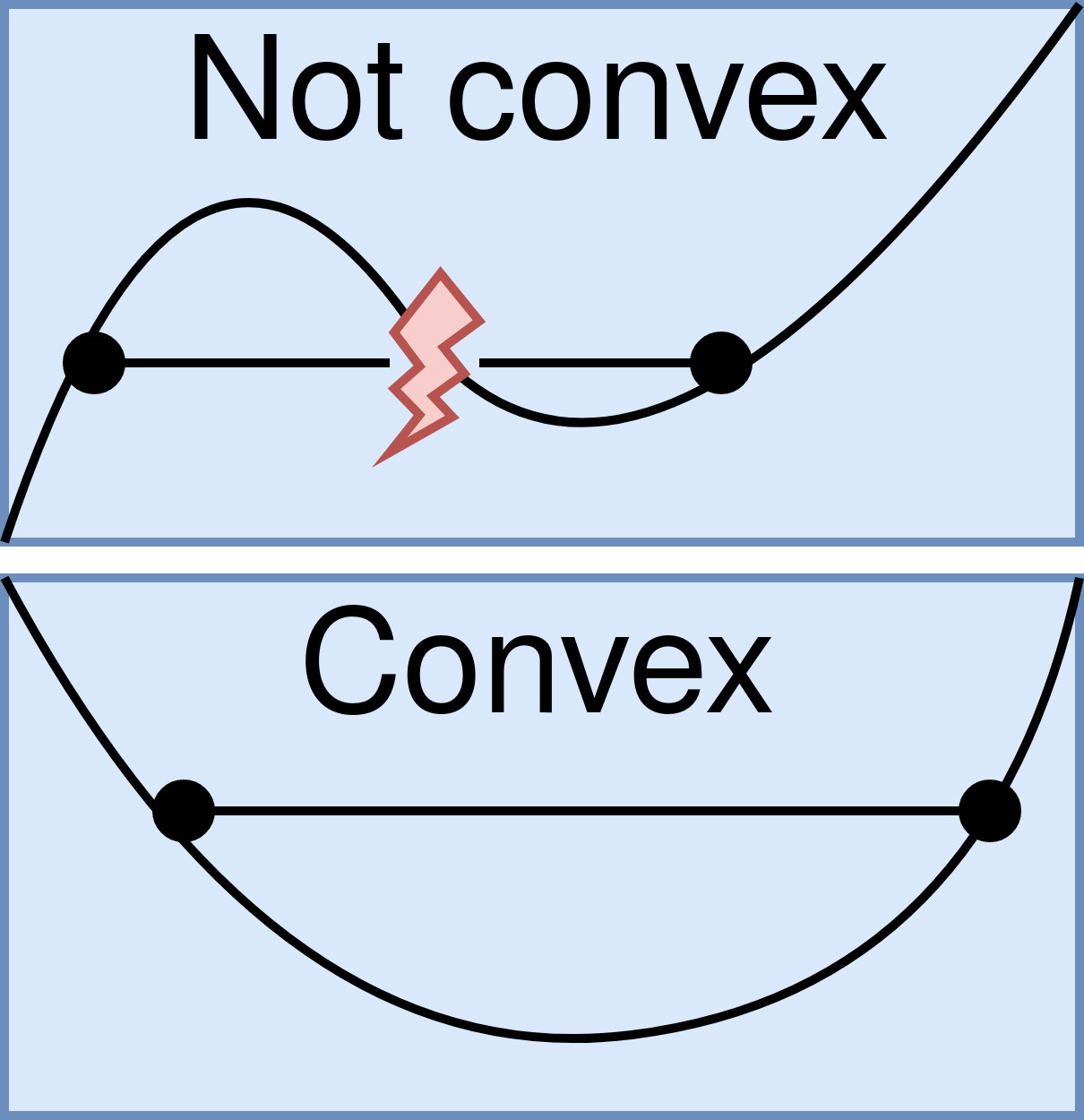
【凸函数第一定义】函数的上图是凸集
- 凸函数的定义域(凸集的投影)一定是凸集
-
【凸函数第二定义】
-
【Jensen不等式】
自变量的凸组合不大于函数值的凸组合
$$ f\left(\alpha \bm x+(1-\alpha)\bm y\right)\le\alpha f(\bm x)+(1-\alpha)f(\bm x). $$
$$ \sum _i p_if(\bm x_i)\ge f(\sum_i p_i\bm x_i) $$
【凸组合】 $\sum_i\alpha_ix_i,\sum_i\alpha_i=1.$
【KL距离 https://en.wikipedia.org/wiki/Kullback–Leibler_divergence】【相对熵】衡量随机事件的距离的唯一方法
-
【严格凸函数】
取严格不等号
-
【强凸函数】
$$ f(\alpha\bm x+(1-\alpha)\bm y)\le \alpha f(\bm x)+(1-\alpha)f(\bm y)-\frac{\alpha(1-\alpha)c}2\lVert\bm x-\bm y\lVert^2 $$
-
【可微凸函数】
-
【不可微函数】一阶次梯度展开https://en.wikipedia.org/wiki/Subderivative
$$ g\in\mathbb R^n $$
-
【一阶充要条件】 【可微凸函数】定义在开凸集上的函数满足任意点函数图像被切平面（大于一阶泰勒展开）支撑，则函数为凸函数
$$ f(y)\ge f(x)+Df(x)(y-x) $$
【不可微函数】
$$ f(y)\ge f(x)+g^T\mid_x(y-x) $$
-
【二阶充要条件】海塞矩阵半正定，则为凸函数
$$ f\in\mathcal C^3 $$
-
-
【保凸运算operations yielding convexity 】
-
非负组合
$$ \sum _{j=1}^mt_jf_j $$
-
取sup最小上界
$$ \sup {j\in J} f_j\\ \cap{j\in J} epi \ f_j $$
-
仿射变换：自变量做仿射变换
$$ g\circ A $$
-
膨胀函数
$$ ug(x/u). $$
-
卷积，最小卷积Min Convolution
-
随约束条件变换的最优解的函数，定义为Ag function。他也是保凸变换
$$ Ag\\ epiger. hull\ of \ A^\prime(epi\ g). $$
-
偏极小
-